Weighting report
The Weight component generates a report in HTML format that can easily be written to a text file. The main report is generated by the
WeightEngine.Execute method. However, additional information (such as information about cases that do not belong in the weighting matrix) is added by the
WeightEngine.Prepare method. You should therefore write the report to the text file twice, once after the call to
WeightEngine.Prepare and once after the call to
WeightEngine.Execute as shown in the
Weighting.dms sample file. For more information, see
Setting up weighting in a DMS file.
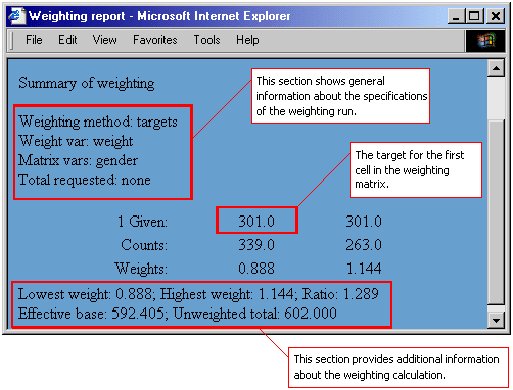
Here is an example of the report for a simple target weighting run based on equal targets of male and female respondents.
For each cell in the weighting matrix, the report shows:
▪Given. The target or factor that was defined
▪Counts. The number of cases that fulfill the requirements of the cell
▪Weights. The weight calculated for the cases in the cell.
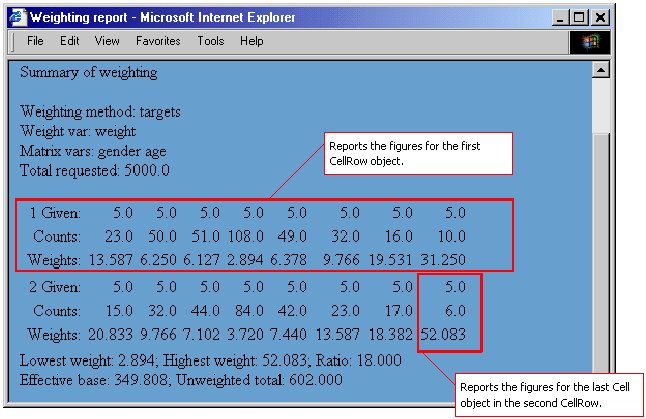
In this report, the weighting was based on one variable that has only two categories and so the weighting matrix has only two cells. Here is another example of the report for a weighting matrix of gender by age and equal targets of respondents in each cell.
In this example, the weighting matrix has been specified in the order gender then age and the report gives the figures for the Male category of the gender variable first and then for the Female category of the gender variable.
If the variables had been specified in the reverse order (
age then
gender) as in the example in
More on target weighting, the table of figures would be rotated.
In addition to this information for each cell in the weighting matrix, the Weight component also reports the following information about the weighting overall:
▪The lowest and highest weights
▪The ratio of the highest weight to the lowest weight
▪The effective base, which is calculated by dividing the squared sum of weights for all of the respondents in the weighting matrix table by the sum of the squared weights
▪The unweighted total
See