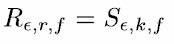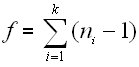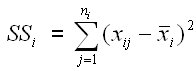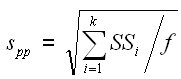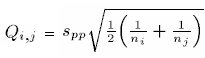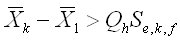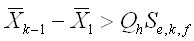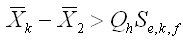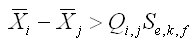|
Notation
|
Description
|
|---|---|
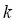 |
Number of levels for an effect.
|
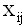 |
j-th observation at i-th level.
|
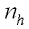 |
Harmonic mean of the sample size.
|
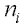 |
Number of observations at level i, i=1,...,k.
|
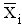 |
Mean at level i, i=1,...,k.
|
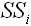 |
Sum of squares at level i, i=1,…k.
|
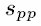 |
Pooled standard deviation from all levels.
|
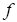 |
Degrees of freedom for the within-groups mean square.
|
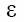 |
Experimentwise error rate under the complete null hypothesis.
|
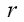 |
Number of steps between means.
|
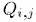 |
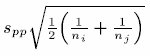 |
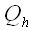 |
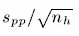 |
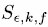 |
The upper-ε critical point of the Studentized range distribution.
|