The base is 43, which is calculated by subtracting the 12 refusal and no answer responses from the total of 55. The median respondent is therefore the 21.5th person, who falls into the ‘201 – 300’ category. There are 13 respondents in this category, and Quantum assumes that they are evenly spread at intervals of 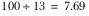 . There are 15 respondents altogether in the previous three categories, so the 21.5th respondent is the 6.5th respondent in the ‘201 – 300’ category, and is at an interval of
. There are 15 respondents altogether in the previous three categories, so the 21.5th respondent is the 6.5th respondent in the ‘201 – 300’ category, and is at an interval of 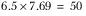 from the end of the previous category, 200. So Quantum adds 50 to 200 to give a median of 250.
from the end of the previous category, 200. So Quantum adds 50 to 200 to give a median of 250.
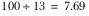 . There are 15 respondents altogether in the previous three categories, so the 21.5th respondent is the 6.5th respondent in the ‘201 – 300’ category, and is at an interval of
. There are 15 respondents altogether in the previous three categories, so the 21.5th respondent is the 6.5th respondent in the ‘201 – 300’ category, and is at an interval of 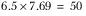 from the end of the previous category, 200. So Quantum adds 50 to 200 to give a median of 250.
from the end of the previous category, 200. So Quantum adds 50 to 200 to give a median of 250.