Statistical formula for the net difference test

Reporter > Applying statistical tests > Net difference test > Statistical formula for the net difference test

The following table shows the formulae used for conducting the net difference test in UNICOM Intelligence Reporter.

Formula for proportions

For any row, and any of the four columns being tested (i=1,2,3, and 4):

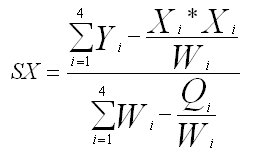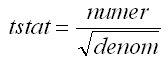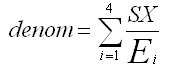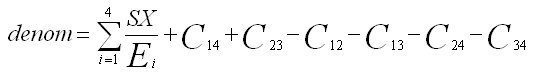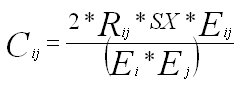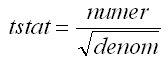
Notation	Description
W i	Sum of the weights (weighted base) for column i.
Q i	Sum of the squared weights for column i.
E i = (W i * W i) / Q i	Effective base for column i.
P i	Proportion in column i

For a table with overlap or a grid table, and any pair of columns from the four being tested (i and j=1,2,3, and 4):

Notation	Description
W ij	Sum of the weights (weighted base) for respondents in both columns.
Q ij	Sum of the squared weights for respondents in both columns.
E ij = (W ij * W ij) / Q ij	Effective base for respondents in both columns.
P ij	Proportion for respondents belonging in the row being tested for both columns.

The formula is:

where

numer = (P 3 - P 4) - (P 1 - P 2)

and for a non-grid, non-overlap table

For a table with overlap or a grid table

where

The degrees of freedom are:

where, for a non-grid, non-overlap table

and

For a table with overlap or a grid table

and

Formula for means

For any row, and any of the four columns being tested (i=1,2,3, and 4):

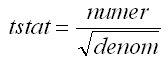
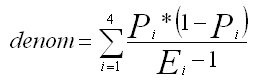
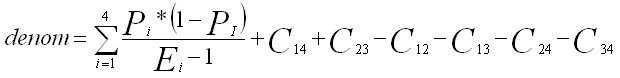
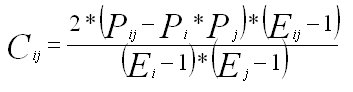
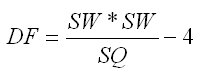
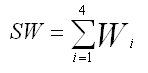
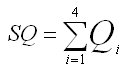
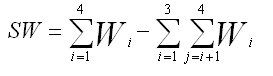
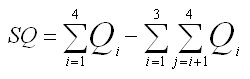
Notation	Description
W i	Sum of the weighted base for column i.
Q i	Sum of the squared weights for column i.
E i = (W i * W i) / Q i	Effective base for column i.
X i	sum of values for column i
Y i	sum of squared values for column i
M i	mean for column i=X i/W i

The values may be either numeric values or factor values.

For a table with overlap or a grid table, and any pair of columns from the four being tested (i and j=1,2,3, and 4):

Notation	Description
W ij	Sum of the weighted base for respondents in both columns
Q ij	Sum of the squared weights for respondents in both columns
E ij = (W ij * W ij) / Q ij	Effective base for respondents in both columns

The intermediate term SX is:

The tstat is

where

numer = (M 3 - M 4) - (M 1 - M 2)

and for a grid, non-overlap table,

For a table with overlap or a grid table

where

For a non-grid table with overlap, R ij reduces to 1.